একাদশ কম্পিউটারকম্পিউটার
নাম্বার সিস্টেম এর ধারাপাত বা সংখ্যা পদ্ধতি – Number System
কম্পিউটার এর ধারাপাত ১ থেকে ১০০

নাম্বার সিস্টেমঃ গনার ইতিহাস চর্চা করলে আমরা দেখতে পাই অতীতকালের মানুষ নিজের আঙুল অথবা নুড়ি ও পাথরের সাহায্যে গুহার গায়ে আঁকা কেটে গণনা করত। সভ্যতার উন্নয়নের সাথে সাথে মানুষ গনার বিভিন্ন পদ্ধতি আবিষ্কার করলো।
নাম্বার সিস্টেম
এই গনার পদ্ধতিকে দুইভাবে ভাগে ভাগ করতে পারি। যথা-
- Non-Positional Number System ( নন- পজিশনাল নাম্বার সিস্টেম )
- Positional Number System ( পজিশনাল নাম্বার সিস্টেম )
Non-Positional Number System (নন- পজিশনাল নাম্বার সিস্টেম)
প্রচিন কালে মানুষ গনার জন্য গুহার গায়ে আঁকা কেটে গণনা করতো। এই প্রকার গনার ক্ষেত্রে সংখ্যার মান তার অবস্থানের ওপর নির্ভর করে না। তাই এই প্রকার সংখ্যা পদ্ধতিকে Non-Positional Number System ( নন- পজিশনাল নাম্বার সিস্টেম ) বলে।
যেমন-
- ১ এর জন্য I
- ২ এর জন্য II
- ৩ এর জন্য III
- ৪ এর জন্য IIII
- ৫ এর জন্য IIIII
- ৬ এর জন্য IIIIII
Positional Number System (পজিশনাল নাম্বার সিস্টেম)
এই প্রকার Number system এর ক্ষত্রে কতগুলি চিহ্ন ও সংখ্যা ব্যবহৃত হয়। অনেকগুলি সংখ্যা পরপর একত্রিত হয়ে একটি সঠিক মানের সংখ্যা গঠন করে এবং প্রত্যেকটি সংখ্যার মান তার অবস্থানের ওপর নির্ভর করে।
যেমন- 234 এই সংখ্যাটি 2,3 ও 4 দ্বারা গঠিত।
এই সংখ্যাটিকে 324,432,342 ইত্যদি ভাবে লিখতে পারি। এতে সংখ্যাটির মানের পরিবর্তন হয়।
- যে নাম্বার সিস্টেমে অঙ্কের অবস্থান পরিবর্তন করলেই সংখ্যাটির মানের পরিবর্তন হয় তাকে Positional Number System (পজিশনাল নাম্বার সিস্টেম) বলে।
বর্তমানে প্রায় সমস্ত গনার কাজে Positional Number System (পজিশনাল নাম্বার সিস্টেম) ব্যবহার করা হয়।
কম্পিউটারে সংখ্যা প্রকাশ করার জন্য মূলত চারতিভাগে সংখ্যা পদ্ধতি ভাগ করা হয়।
যথা —
- দশমিক সংখ্যা পদ্ধতি (Decimal Number system)
- বাইনারি সংখ্যা পদ্ধতি (Binary Number System),
- অক্টাল সংখ্যা পদ্ধতি (Octal Number System) এবং
- হেক্সাডেসিমাল সংখ্যা পদ্ধতি (Hexadecimal Number System)
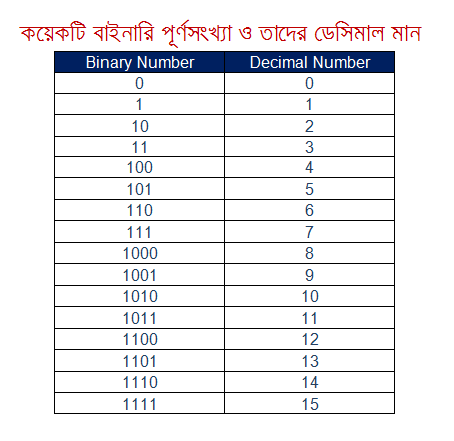
বাইনারি নাম্বার সিস্টেম (Binary Number System) :
বাইনারি নাম্বার সিস্টেম বা বাইনারি সংখ্যা পদ্ধতিতে কেবলমাত্র দুটি মূল সংখ্যা ব্যবহার করা হয় — 0 এবং 1। সেই জন্য এই নাম্বার সিস্টেম-এর বেস (Base) হল 2. এই নাম্বার সিস্টেম এ 0 এবং 1 ছাড়া অন্য কোনো সংখ্যার ব্যবহার হয় না। দুটি মূল সংখ্যা 0 এবং 1 কে বলা হয় বাইনারি ডিজিট (Binary Digits) বা বিট (Bit)। ৮ টি বিট কে একসাথে বলা হয় বাইট (Byte) এবং ৪ টি বিট কে একসাথে বলা হয় নিবিল (Nibble)।
বাইনারি সংখ্যা পদ্ধতিতে কোনো পূর্ণসংখ্যা কে পরপর কতকগুলি 0 এবং 1 দিয়ে প্রকাশ করা হয়। যেমন – 1010, 1001, 0000, 0001 ইত্যাদি।
আবার বাইনারি সংখ্যা পদ্ধতিতে কোনো ভগ্নাংশ কে প্রকাশ করার জন্য দশমিক বিন্দুর পরে ডিজিট গুলি লেখা হয়। যেমন – 0.1011, 0.111 ইত্যাদি।
ডেসিমাল নাম্বার সিস্টেম (Decimal Number System) :
ডেসিমাল নাম্বার সিস্টেম বা ডেসিমাল সংখ্যা পদ্ধতিতে মোট দশটি সংখ্যা আছে — 0, 1, 2, 3, 4, 5, 6, 7, 8, এবং 9. এই নাম্বার সিস্টেম -এর বেস (Base) হল 10. ডেসিমাল সংখ্যার উদাহরন হল পূর্ণসংখ্যা : 2354, 10101, 1234 এবং ভগ্নাংশ : 0.111, 0.3521 ইত্যাদি।
কোনো পূর্ণসংখ্যার একেবারে বামদিকে যে সংখ্যাটি থাকে তাকে বলা হয় Most Significant Digit বা MSD এবং একেবারে ডানদিকে যে সংখ্যাটি থাকে তাকে বলা হয় Least Significant Digit বা LSD.
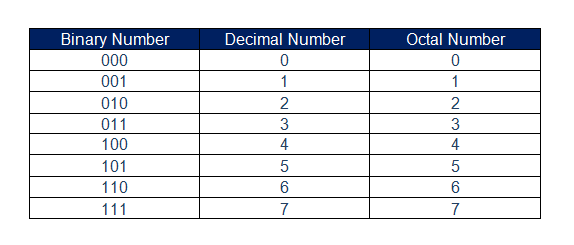
অক্টাল নাম্বার সিস্টেম (Octal Number System):
অক্টাল নাম্বার সিস্টেম বা অক্টাল সংখ্যা পদ্ধতিতে আটটি (8) মূল সংখ্যা ব্যবহার করা হয়। সংখ্যাগুলি হল 0, 1, 2, 3, 4, 5, 6, এবং 7. এই সংখ্যা পদ্ধতির বেস হল 8 (Eight). উদাহরন – 1001, 2541 ইত্যাদি।
হেক্সাডেসিমাল নাম্বার সিস্টেম (Hexadecimal Number System) :
হেক্সাডেসিমাল নাম্বার সিস্টেম বা হেক্সাডেসিমাল সংখ্যা পদ্ধতিতে ষোল (16)-টি মূল সংখ্যা ব্যবহার করা হয়। তাই এই নাম্বার সিস্টেম-এর বেস হল 16 (Sixteen). এই ষোল (16)-টি সংখ্যা হল 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E এবং F. এখানে A, B, C, D, E এবং F হল সংখ্যা অক্ষর না।
A=10, B=11, C=12, D=13, E=14 ও F=15.
হেক্সাডেসিমাল সংখ্যার উদাহরন হল পূর্ণসংখ্যা : BCA, 10101, 1234, 52D4 এবং ভগ্নাংশ : 0.F41 ইত্যাদি
নাম্বার সিস্টেম এর ধারাপাত
| Decimal | Binary | Octal | Hexa Decimal |
| 1 | 1 | 1 | 1 |
| 2 | 10 | 2 | 2 |
| 3 | 11 | 3 | 3 |
| 4 | 100 | 4 | 4 |
| 5 | 101 | 5 | 5 |
| 6 | 110 | 6 | 6 |
| 7 | 111 | 7 | 7 |
| 8 | 1000 | 10 | 8 |
| 9 | 1001 | 11 | 9 |
| 10 | 1010 | 12 | A |
| 11 | 1011 | 13 | B |
| 12 | 1100 | 14 | C |
| 13 | 1101 | 15 | D |
| 14 | 1110 | 16 | E |
| 15 | 1111 | 17 | F |
| 16 | 10000 | 20 | 10 |
| 17 | 10001 | 21 | 11 |
| 18 | 10010 | 22 | 12 |
| 19 | 10011 | 23 | 13 |
| 20 | 10100 | 24 | 14 |
| 21 | 10101 | 25 | 15 |
| 22 | 10110 | 26 | 16 |
| 23 | 10111 | 27 | 17 |
| 24 | 11000 | 30 | 18 |
| 25 | 11001 | 31 | 19 |
| 26 | 11010 | 32 | 1A |
| 27 | 11011 | 33 | 1B |
| 28 | 11100 | 34 | 1C |
| 29 | 11101 | 35 | 1D |
| 30 | 11110 | 36 | 1E |
| 31 | 11111 | 37 | 1F |
| 32 | 100000 | 40 | 20 |
| 33 | 100001 | 41 | 21 |
| 34 | 100010 | 42 | 22 |
| 35 | 10011 | 43 | 23 |
| 36 | 100100 | 44 | 24 |
| 37 | 100101 | 45 | 25 |
| 38 | 10010 | 46 | 26 |
| 39 | 100111 | 47 | 27 |
| 40 | 101000 | 50 | 28 |
| 41 | 101001 | 51 | 29 |
| 42 | 101010 | 52 | 2A |
| 43 | 101011 | 53 | 2B |
| 44 | 101100 | 54 | 2C |
| 45 | 101101 | 55 | 2D |
| 46 | 101110 | 56 | 2E |
| 47 | 101111 | 57 | 2F |
| 48 | 110000 | 60 | 30 |
| 49 | 110001 | 61 | 31 |
| 50 | 110010 | 62 | 32 |
| 51 | 110011 | 63 | 33 |
| 52 | 110100 | 64 | 34 |
| 53 | 110101 | 65 | 35 |
| 54 | 110110 | 66 | 36 |
| 55 | 111000 | 67 | 37 |
| 56 | 111000 | 70 | 38 |
| 57 | 111010 | 71 | 39 |
| 58 | 111011 | 72 | 3A |
| 59 | 1111011 | 74 | 3B |
| 60 | 111100 | 75 | 3C |
| 61 | 111101 | 75 | 3D |
| 62 | 111110 | 76 | 3E |
| 63 | 111111 | 77 | 3F |
| 64 | 1000000 | 100 | 40 |
| 65 | 1000001 | 101 | 41 |
| 66 | 1000010 | 102 | 42 |
| 67 | 1000011 | 103 | 43 |
| 68 | 1000100 | 104 | 44 |
| 69 | 1000101 | 105 | 45 |
| 70 | 1000110 | 106 | 46 |
| 71 | 1000111 | 107 | 47 |
| 72 | 1001000 | 110 | 48 |
| 73 | 1001001 | 111 | 49 |
| 74 | 1001010 | 112 | 4A |
| 75 | 1001011 | 113 | 4B |
| 76 | 1001100 | 114 | 4C |
| 77 | 1001101 | 115 | 4D |
| 78 | 1001110 | 116 | 4E |
| 79 | 1001111 | 117 | 4F |
| 80 | 1010000 | 120 | 50 |
| 81 | 1010001 | 121 | 51 |
| 82 | 1010010 | 122 | 52 |
| 83 | 1010011 | 123 | 53 |
| 84 | 1010100 | 124 | 54 |
| 85 | 1010101 | 125 | 55 |
| 86 | 1010110 | 126 | 56 |
| 87 | 1010111 | 127 | 57 |
| 88 | 1011000 | 131 | 58 |
| 89 | 1011001 | 132 | 59 |
| 90 | 1011010 | 133 | 5A |
| 91 | 1011011 | 134 | 5B |
| 92 | 1011100 | 135 | 5C |
| 93 | 1011101 | 136 | 5D |
| 94 | 1011110 | 137 | 5E |
| 95 | 1011111 | 137 | 5F |
| 96 | 1100000 | 140 | 60 |
| 97 | 1100001 | 141 | 61 |
| 98 | 1100010 | 142 | 62 |
| 99 | 1100011 | 143 | 63 |
| 100 | 1100100 | 144 | 64 |
| 101 | 1100101 | 145 | 65 |
এটিও পড়ুন –কম্পিউটার সাধারন সমস্যা এবং তাদের সমাধান
এগুলিও পড়তে পারেন -

 Search 10000+ Jobs | Any Qualification | Fresher | Full time Jobs| Part Time Jobs And More (Check Now)
Search 10000+ Jobs | Any Qualification | Fresher | Full time Jobs| Part Time Jobs And More (Check Now)